Please Follow This Link to Our New Updated Research Page

Spintronics and Nanomagnetism Investigation of Magnetic Semiconductor Nanomaterials

As consumers of high-tech semiconductor technology, we have become accustomed to faster and smaller products with each new generation of computers, ipods, smart phones, etc. However, the current fabrication methods and device architectures that have enabled this rapid progress are quickly approaching their physical limits. Spintronics, or spin based electronics, attempts to manipulate the spin degree of freedom, instead of or in addition to the charge of electrons to create new functionality and prolong this era of rapid technological advancement. The field of spintronics has already produced several major advances, the most famous being the giant magnetoresistive (GMR) effect which is the primary operating principle behind current hard-drive technology and also the subject of the 2007 Nobel Prize in physics. Future development of spintronics envisions the integration of semiconductor device function with magnetic storage, such as in a spin-transistor [1] or a spin-LED, which will revolutionize computing by offering the advantages of nonvolatility, faster data processing speed, low power consumption, and high integration densities. This demands significant advances in magnetic semiconducting materials.

Synthesis of magnetic semiconductor nanomaterials

The Jin Group specializes in the development of novel synthetic methods and in the rational synthesis of new nanomaterials. We have synthesized concentrated magnetic semiconducting nanomaterials, such as nanocrystals of EuS,[2] GdS and Eu1-xGdxS alloys,[3] as well as nanowires of EuO,[4] CrO2,[5] Fe1-xCoxSi[6-7] and MnSi.[8] These materials offer promise for fundamental investigation and demonstrations of 1-D nanodevices. Many of these magnetic materials have critical temperatures well below liquid nitrogen temperatures and will be important for studies of fundamental physics, however future applications will require higher operating temperatures. We therefore continue efforts to synthesize one-dimensional silicide and germanide materials with higher critical temperatures such as MnGe, FeGe, and alloys therein.

The exotic Skyrmion magnetic ordering in B20 silicides

We are also working on understanding the electronic and magnetic properties of these nanomaterials. Fe1-xCoxSi and MnSi belong to the B20 cubic crystal system that lacks a center of inversion symmetry, and this particular crystal system has recently been discovered to exhibit exotic configurations of spin alignment such as helimagnetism and the Skyrmion lattice (see Figure 1). Magnetic Skyrmions can be thought of as whirlpool-like configurations of spin (Figure 1b). These spin domains are topologically
stable, meaning they can act as individual particle-like domains and they are stable against small fluctuations in temperature and field. One intriguing consequence of this topological stability is an associated effective magnetic field that results in some newly observed and relatively under-studied phenomena known collectively as emergent electrodynamics. In the case of a Skyrmion lattice induced to translational motion by an applied current, an electric field is generated transverse to the applied current due to the effective field associated with the Skyrmion lattice and this electric field can be exploited to study important dynamical effects through all-electrical schemes.

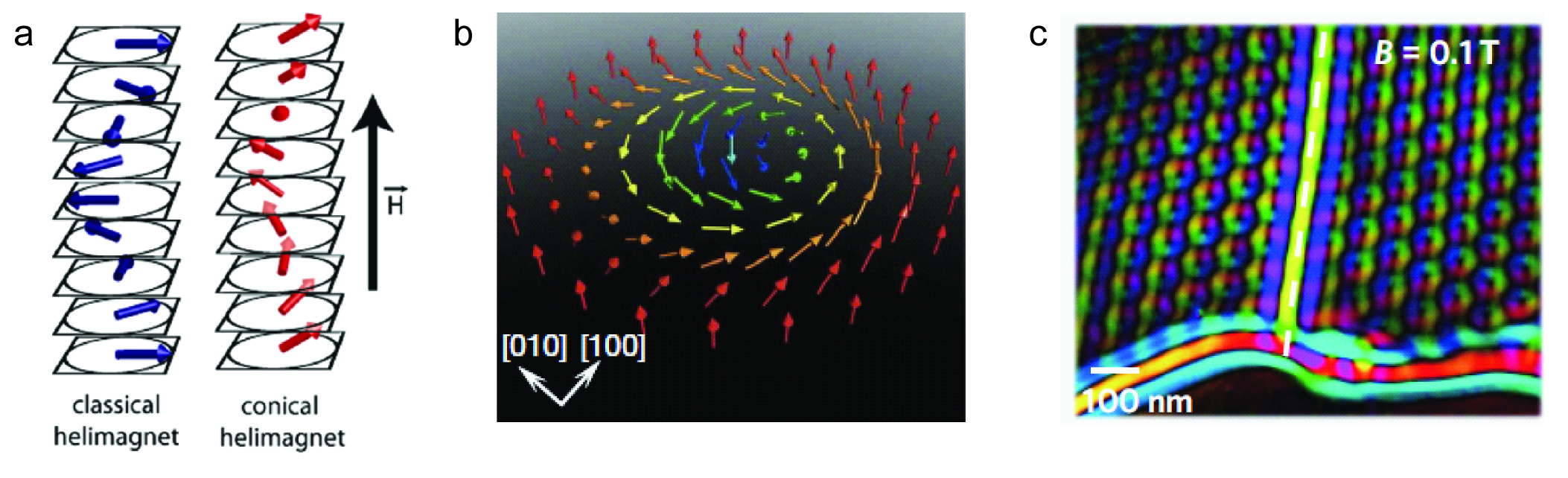
 Figure 1. a) Schematic spin configurations of a classical helimagnet and the subsequent formation of a conical helimagnet in an externally applied magnetic field.[8] b) Schematic of a magnetic Skyrmion domain depicting the whirling spin configuration. c) Colorized Lorentz TEM image showing the magnetic Skyrmion lattice phase with a phase boundary in a FeGe thin film sample.[9] 

Investigation of nanowire devices for future magnetic storage devices

Until recently, observational studies of the helimagnetic and Skyrmion phases were limited to bulk and thin film materials due to the limitations of Lorentz TEM and neutron scattering experiments.[10-12] Most recently, we collaborated with Prof. Tokura’s lab in the University of Tokyo and RIKEN to successfully observe the magnetic skyrmion phase in a MnSi nanowire that was shaped into a thin slab using a focused-ion beam (Figure 2a).[13] The skyrmion phase was observed between 6 K and 35 K (as shown in Figures 2b, 2c), which is a much larger temperature window than the skyrmion lattice phase observed in bulk MnSi (27- 29.5 K).

Figure 2. Lorentz TEM observation of a MnSi nanowire.[13] a) A scanning electron micrograph of the final MnSi nanowire sample thinned with a focused ion-beam. b) Colorized Lorentz TEM image showing the in-plane magnetization direction with the characteristic hexagonal packing of the skyrmion lattice phase. c) Magnetic phase diagram of the MnSi nanowire constructed using the temperature and magnetic field points indicated by open circles, with the black boundary lines indicating the approximate phase boundaries between magnetic phases.

The recently revealed electrical signature of the Skyrmion phase can provide a pathway to study these phases in nanowire morphology. We have been working on alternative experimental probes using electrical transport measurements to confirm the signatures of skyrmion magnetic domains. Our group has significant experience measuring electrical and magnetic phenomena on nanowire heterostructures, for instance, we have developed the technique of Andreev reflection spectroscopy to measure the spin-polarization of Fe1-xCoxSi nanowires (Figure 3).[14] Furthermore, the magnetic Skyrmion domain is of particular interest for the newly proposed concepts of racetrack memory [15] that utilize spin-torque transfer effects to manipulate the motion of these magnetic domains for high-density, low-power, and non-volatile memory technology. Importantly, recent studies suggest that the Skyrmion phase is further stabilized by dimensional confinement [9, 16-17] and therefore our nanowire materials offer a natural platform for implementing magnetic Skyrmions in such a racetrack memory device. We have successfully identified the electrical signature of helimagnetism in MnSi nanowires (Figure 4) and found that the transition temperature is higher by 5 K, suggesting that these exotic spin textures are stabilized by confinement in nanowire morphology.[8] We are actively exploring new device concepts and measurement techniques to identify the Skyrmion phase and understand the fundamental physics and suitability of these exotic spin configurations for future spintronic devices.

Figure 3. Measuring spin polarization using Andreev reflection spectroscopy. a) Schematic cross-section view of the two-probe nanowire device geometry and measurement setup. b) Band diagram of the interface between a spin-polarized conductor and a superconductor. The availability of spin up and spin down carriers directly affects the formation of Cooper pairs and can be measured in a differential conductance spectrum. c) Example differential conductance spectrum for a Fe1-xCoxSi nanowire device and the best fit to the Blonder-Tinkham-Klapwijk model used to extract a spin polarization of 35%.[14]

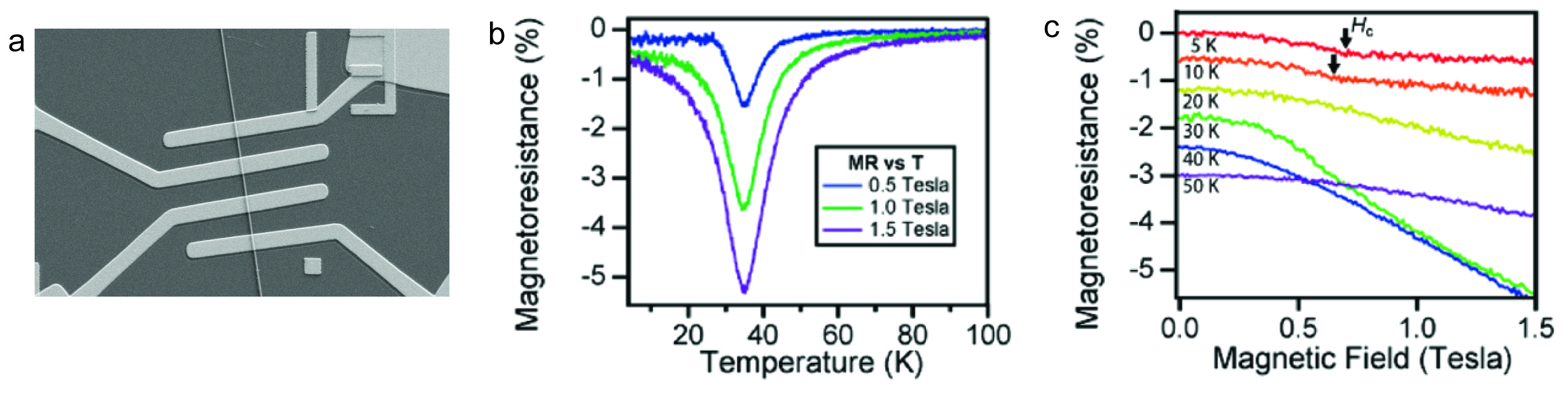
Figure 4. a) Scanning electron micrograph of a typical four-probe nanowire device fabricated using common electron beam lithography techniques. b) Magnetoresistance as a function of temperature measured on a MnSi nanowire. The peak at 35 K corresponds to the critical temperature for the helimagnetic phase. c) Magnetoresistance as a function of applied magnetic field for various temperatures with arrows showing the kink corresponding to the reorientation of the helimagnetic phase to the conical phase.[8]

References
1. Datta, S.; Das, B., Appl. Phys. Lett. 1990, 56 (7), 665.
2. Selinsky, R. S.; Keavney, D. J.; Bierman, M. J.; Jin, S., Appl. Phys. Lett. 2009, 95 (20), 202501/1-202501/3.
3. Selinsky Rachel, S.; Han Jae, H.; Morales Perez Elvin, A.; Guzei Ilia, A.; Jin, S., J. Am. Chem. Soc. 2010, 132 (45), 15997-6005.
4. Bierman, M. J.; Van Heuvelen, K. M.; Schmeisser, D.; Brunold, T. C.; Jin, S., Adv. Mater. 2007, 19 (18), 2677-2681.
5. Song, Y.; Schmitt, A. L.; Jin, S., Nano Lett. 2008, 8 (8), 2356-2361.
6. In, J.; Varadwaj, K. S. K.; Seo, K.; Lee, S.; Jo, Y.; Jung, M.-H.; Kim, J.; Kim, B., J. Phys. Chem. C 2008, 112 (12), 4748-4752.
7. Higgins, J. M.; Carmichael, P.; Schmitt, A. L.; Lee, S.; Degrave, J. P.; Jin, S., ACS Nano 2011, 5 (4), 3268-3277.
8. Higgins, J. M.; Ding, R.; DeGrave, J. P.; Jin, S., Nano Lett. 2010, 10 (5), 1605-1610.
9. Yu, X. Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W. Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y., Nature Mater. 2011, 10 (2), 106-109.
10. Uchida, M.; Onose, Y.; Matsui, Y.; Tokura, Y., Science 2006, 311 (5759), 359-361.
11. Muhlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Boni, P., Science 2009, 323 (5916), 915-919.
12. Yu, X. Z.; Onose, Y.; Kanazawa, N.; Park, J. H.; Han, J. H.; Matsui, Y.; Nagaosa, N.; Tokura, Y., Nature 2010, 465 (7300), 901-904.
13. Yu, X.; DeGrave, J. P.; Hara, Y.; Hara, T.; Jin, S.; Tokura, Y.; Nano Lett. 2013, 13, 3755-3759.
14. DeGrave, J. P.; Schmitt, A. L.; Selinsky, R. S.; Higgins, J. M.; Keavney, D. J.; Jin, S., Nano Lett. 2011, 11 (10), 4431-4437.
15. Parkin, S. S. P.; Hayashi, M.; Thomas, L., Science 2008, 320 (5873), 190-194.
16. Tonomura, A.; Yu, X.; Yanagisawa, K.; Matsuda, T.; Onose, Y.; Kanazawa, N.; Park, H. S.; Tokura, Y., Nano Lett. 2012, 1673–1677.
17. Huang, S. X.; Chien, C. L., Phys. Rev. Lett. 2012, 108 (26), 267201/1-267201/5.