Magnetic Skyrmions in Nanowires for Spintronic Devices
Spintronics and Magnetic Skyrmions
As consumers of high-tech semiconductor technology, we have become accustomed to faster and smaller products with each new generation of computers, ipods, smart phones, etc. However, the current fabrication methods and device architectures that have enabled this rapid progress are quickly approaching their physical limits. Spintronics, or spin based electronics, attempts to manipulate the spin degree of freedom, instead of or in addition to the charge of electrons to create new functionality and prolong this era of rapid technological advancement. The field of spintronics has already produced several major advances, the most famous being the giant magnetoresistive (GMR) effect which is the primary operating principle behind current hard-drive technology and also the subject of the 2007 Nobel Prize in physics. The recent emergence of magnetic skyrmions provides us new ideas for spintronic and magnetic storage devices.
Magnetic Skyrmions are recently discovered exotic vortex-like magnetic spin textures in which the central spin is anti-aligned with the externally applied magnetic field and the outer spins are aligned (Fig. 1A).1 The formation of magnetic skyrmions results from the competition of the ferromagnetic exchange and the Dzyaloshinskii-Moriya (DM) interaction that appears in crystal systems lacking a center of inversion symmetry, such as the non-centrosymmetric cubic B20 crystal system, including MnSi, Fe1-xCoxSi, FeGe, and MnGe.1 The materials that host skyrmions have been studied using small-angle neutron scattering (SANS), Lorentz transmission electron microscopy (LTEM), magnetization, and magneto-transport measurements to confirm the skyrmion lattice phase and map out the magnetic phase diagrams (an example for MnSi is shown in Fig. 1C). Under SANS, a hexagonally closed packed lattice of skyrmions leads to a six-fold diffraction pattern (see Fig. 1D for MnSi).2 Perhaps the most beautiful and direct evidence for skyrmion magnetic domains is the real space imaging via Lorentz TEM which allows the observation of the in-plane magnetization of thin film samples in real-space. In LTEM, a helimagnetic texture appears as a striped pattern, while a skyrmion appears as a vortex (Fig. 1B).1 Furthermore, the observations of the topological Hall effect (THE) beyond the normal Hall effect and anomalous Hall effect through Hall effect measurements have been considered as an electrical transport signature of skyrmions.1 This is because when a conduction electron passes through a topologically non-trivial spin texture, the spin of the conduction electron adiabatically couples to the local spins (Fig. 2A) and acquires a quantum-mechanical Berry phase that can be re-formulated in terms of an effective magnetic field, which deflects the conduction electrons perpendicular to the current direction (Fig. 2B).1 Therefore, the presence of skyrmions will cause an additional contribution to the observed Hall signal which has been termed THE.

Fig. 1. A) Schematic of a magnetic skyrmion (with effective field, Beff); B) A real space observation of the spin states of skyrmion by Lorentz TEM; C) The experimental magnetic phase diagram derived from SANS and magnetization experiments, and D) six-fold SANS diffraction pattern of the skyrmion lattice in MnSi crystals.1,2
The Applications of Skyrmions in Magnetic Racetrack Memory Devices
Due to the topologically non-trivial whirlpool-like spin arrangements, skyrmions can be thought about as free particle-like isolated magnetic domains that are stable against small perturbations in magnetic field and temperature. The fact that skyrmions interact strongly with conduction electrons (Fig. 2A) makes them useful for spintronic applications.3 Skyrmion domains can be driven (Fig. 2B) via spin transfer torque under remarkably low current densities compared to traditional ferromagnetic domain walls.2,3 Our research group confirmed the current-driven motion of skyrmions in NWs using THE measurements.4 These experiments showed that skyrmion domains translate primarily along the current direction at a current density on the order of 106-107 A m-2, which is up to 4-5 orders of magnitude smaller than the current densities required for the translation of ferromagnetic domain walls (1010-1011 A/m2).4 The relative stability and ease of manipulating magnetic skyrmions with electrical current result from their non-trivial topology, smoothly varying spin configuration, and unique ability to deform and avoid pinning sites.1
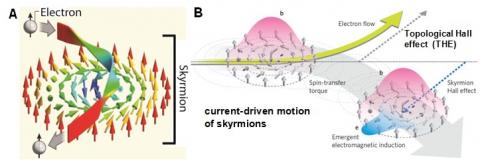
Fig. 2. A) Schematic of electron motion as it traverses a skyrmion spin texture. B) Motion of skyrmions driven by an applied current and the topological Hall effect (THE).1
Skyrmions have a strong analogy to the domains in metallic ferromagnets that have been studied for magnetic racetrack memory architectures. In a magnetic racetrack memory device (Fig. 3), information is encoded in a train of up and down magnetic domains separated by domain walls.5 Conceptually, magnetic domains to which the information is coded are initiated and controlled using current pulses and patterned into a magnetic material that makes up the “racetrack.” Spin polarized current pulses then push the magnetic domains along the racetrack via the spin-transfer torque mechanism until they reach a magnetic domain sensing element. So far the vast majority of research on magnetic racetrack memory has been on ferromagnetic NWs such as permalloy.6 However, the domain walls in these ferromagnetic systems pin strongly to defects and often require current densities in excess of 1010 A/m2 to manipulate the domain-walls which causes excessive Joule heating, ultimately leading to device failure.6

Fig. 3. Schematic of magnetic racetrack memory device. Adapted from ref. [7].
To explore skyrmions for potential magnetic storage technology, we need to study the stability and dynamics of skyrmions in skyrmion-hosting nanoscale systems. In fact, NWs should stabilize the skyrmion phases more so than in the bulk and thin films.8 As the dimension of the system approaches the size of the skyrmion domains, the conical magnetic configuration will be destabilized energetically compared to the skyrmion state.8 This has been both theoretically and experimentally shown repeatedly in several B20 materials with nanoscale dimensions.1 Moreover, NWs with diameter comparable to the skyrmion domain size could emphasize the quantized responses of discrete and isolated skyrmion domains, possibly down to single skyrmions. Furthermore, a NW can be the “racetrack” for the skyrmion motion. Our studies of skyrmions in NWs are enabled by the chemically synthesized single-crystal metal silicide and germanide NWs that we have developed over the last decade.9 We have developed a unique approach of utilizing single source organometallic precursors for chemical vapor deposition (CVD) synthesis and a complementary chemical vapor transport (CVT) method, and succeeded in growing single-crystal NWs of the skyrmion-hosting B20 monosilicide (i.e. MnSi)10 and alloy NWs with controllable amount of dopants (e.g. Fe1-xCoxSi).11 Using these existing NW materials, we have studied the physics and devices of NWs, as discussed below.
Lorentz TEM Observation of Skyrmions in MnSi Nanowires.
In collaboration with Prof. Tokura at the Univeristy of Tokyo, we have made real-space observation of skyrmions and helical magnetic domains in a MnSi NW using Lorentz TEM.12 The MnSi NW was thinned to a rectangular cross-section by focused-ion beam (FIB) milling (Fig. 4a) to reduce obstructive Fresnel fringes. Helimagnetic domains, imaged as alternating bright and dark contrast stripes with an 18 nm period were observed to be the spontaneous magnetic ground state at 6 K, while the hexagonal skyrmion lattice (SkX) with a domain diameter of 18 nm was observed under a normal magnetic field of 210 mT (Fig. 4b). Temperature dependent measurements revealed that the SkX is stable over a larger temperature range in this NW (6 K – 35 K, Fig. 4C) compared with the narrow temperature regime of skyrmion phase in bulk MnSi (26 - 30 K, see Fig. 1C) and thin films of MnSi (5 - 23 K).
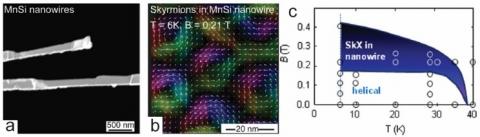
Fig. 4. a) A SEM of the FIB-thinned NW slab; b) Colorized Lorentz TEM image showing the in-plane magnetization direction with the hexagonal packing of the skyrmion lattice phase. c) Magnetic phase diagram of the MnSi NW constructed from data points acquired using Lorentz TEM (open circles).12
Detection and Manipulation of Skyrmions in MnSi NWs Using Topological Hall Effect.
After we observed the existence and confirmed the stabilization of skyrmions in MnSi NWs using Lorentz TEM, we sought to electrically detect their transport signatures using magneto-transport and Hall effect measurements, and eventually tried to manipulate these magnetic domains using electrical devices. Particularly the observation of an extra component of Hall effect, termed “topological Hall effect” (THE) that originates from the topological nature of skyrmions, is the electrical signature of skyrmions. We first developed a general methodology for measuring the Hall effect on 1D NW morphology by fabricating side-wall Hall probe contacts (Fig. 5A, B) using an elaborate multi-step angled evaporation procedure to achieve good side-wall contact.13 Building on and further perfecting this method to achieve better signal-to-noise ratio and developing the data analysis procedures, we were able to extract the topological Hall resistivity (rhoTyx) signal from MnSi NWs. As shown in Fig. 5C, the THE was observed in an extended magnetic field-temperature window (15 to 30 K), confirming the stabilization of skyrmion phase in NWs compared with the bulk (27 to 29.5 K).4

Fig. 5. (A) Schematic and (B) SEM image of the MnSi NW Hall device. (C) Phase diagrams constructed from extracted Hall resistivity as a function of the external magnetic field (B) and temperature (T) for a MnSi NW, which shows extended T-H stability region for skyrmions in comparison with the bulk phase diagram.4
Furthermore, for the first time, the current-driven dynamics of skyrmions was studied in this extended skyrmion phase region and it was found that under the high current density of 108-109 Am-2 enabled by NW geometry, the THE decreases with increasing current densities (Fig. 6A), which demonstrates the current-driven motion of skyrmions generating the emergent electric field.4 We have confirmed the THE signal depends on 1/j where j is the current density in the NW device (Fig. 6B). By following and modifying the theoretical model developed on the current-driven movement of skyrmions, we can fit the data and extract the skyrmion drifting velocity (vd). We also found that above the critical current density (jc) of about 107 Am-2, the vd is linearly proportional to current density (Fig. 6C).4 This study provides the confirmation and knowledge base for motion of skyrmions in NWs and opens up the exploration of skyrmion-based racetrack memory.

Fig. 6. Topological Hall resistivity (rhoTyx) of MnSi NWs as a function of current density (j). A) rhoTyx vs. B at T = 24.12 K and B) rhoTyx vs. j at T = 22.04 and 24.12 K under increasing current densities from j = 6.87×108 to 27.5×108 A m-2. C) Estimated skyrmion drift velocity (vd) as a function of current density (j).4
Magnetoresistance Studies and Cascading Quantized Transitions of Skyrmion Cluster States in MnSi Nanowires.
In collaboration with Prof. Mingliang Tian at Chinese Academy of Sciences, we used focused ion beam (FIB) to fabricate 4-probe devices using the MnSi NWs and carried out complementary magneto-transport measurements to study the skyrmion physics. We first demonstrated that the skyrmion state in helimagnetic MnSi NWs with varied diameters from 400 nm to 250 nm can exist in a substantially extended T-H region.14 MR measurements under a moderate external magnetic field along the long axis of the NWs (H‖) show transitions corresponding to the skyrmion state from Tc ~32 K down to at least 3 K. Then, we focused on MnSi NWs with small (< 100 nm) diameters that can be selected using a micromanipulator. We have observed magnetic field-driven cascading quantized transitions of skyrmion cluster states in these thinner MnSi NWs using refined magneto-transport measurements.15 With the ultra-narrow MnSi NWs with diameters around 40 nm, we observed quantized jumps in MR versus magnetic field curves (Fig. 7A). By tracking the size dependence of the jump number, we infer that skyrmions are assembled into cluster states with a tunable number of skyrmions, in agreement with Monte Carlo simulations (Fig. 7B). Our results, together with another recent study using THE measurements on etched FeGe nanostructure,16 clearly demonstrate that skyrmions can exist in discrete numbers from single to several skyrmions and simple MR measurement can enable an electric reading of the number of skyrmions in the cluster states.15 These results show that it is possible to realize memory devices based on isolated few skyrmions.

Fig. 7. A) The observed transitions of magnetoresistance of a MnSi NW with a diameter of ~ 40 nm and B) the corresponding illustration of the calculated spin states of the various skyrmion cluster states.14
We collaborated with Prof. Martino Poggio at University of Basel, Switzerland on using their unique dynamic cantilever magnetometry technique to investigate the magnetic behaviors and skyrmion physics in MnSi NWs. Magnetization measurements are arguably the most direct probe of the magnetic phase transitions, however, measurements of individual NWs are not possible by conventional techniques due to their small total magnetic moment. For such individual nanostructures, dynamic-mode cantilever magnetometry developed by Prof. Poggio is an ideal method for investigating the magnetization in various magnetic field orientations. Using cantilever magnetometry of mounted MnSi NWs, we measured an enhanced skyrmion lattice phase extending from T = 29 K down to at least T = 0.4 K in MnSi NWs (Fig. 8).17 These results further confirm the conclusions from the Lorentz TEM, THE, and MR measurements discussed above, but provide more subtle and fundamental details about the nature of the stabilization of skyrmions in NWs. The stability of the skyrmion phase depends on the orientation of the NWs with respect to the applied magnetic field, suggesting that magnetic anisotropy induced by surface effect is responsible for the stabilization. The additional transitions observed by cantilever magnetometry (Fig. 8) also suggest the existence of disordered skyrmions (skyrmion liquids) or isolated skyrmions in addition to the well-ordered skyrmion lattice (SkX).

Fig. 8. Scheme of the dynamic cantilever magnetometry measurement of NWs and the magnetic phase diagrams determined for a single MnSi NW using this technique.17
Building on these past achievements and new nanowires of B20 silicides and germanides, we are currently working on fabricating and measuring nanodevices to create, manipulate, and detect isolated magnetic skyrmions in nanowires. The success of our studies will demonstrate the feasibility for magnetic memory devices based on skyrmions and lay the foundation for a future “skyrmionics” technology. They will open up new design concepts for developing novel spintronic devices with low-power, enhanced performance, and therefore bring broad technological impacts.
References
1) Nagaosa, N.; Tokura, Y., Topological properties and dynamics of magnetic skyrmions; Nature Nanotechnology 2013, 8, 899.
2) Muhlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Boni, P., Skyrmion Lattice in a Chiral Magnet; Science 2009, 323, 915.
3) Schulz, T.; Ritz, R.; Bauer, A.; Halder, M.; Wagner, M.; Franz, C.; Pfleiderer, C.; Everschor, K.; Garst, M.; Rosch, A., Emergent electrodynamics of skyrmions in a chiral magnet; Nat. Phys. 2012, 8, 301.
4) Liang, D.; DeGrave, J. P.; Stolt, M. J.; Tokura, Y.; Jin, S., Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect; Nature Communications 2015, 6, 8217.
5) Parkin, S. S. P.; Hayashi, M.; Thomas, L., Magnetic domain-wall racetrack memory; Science 2008, 320, 190.
6) Pulizzi, F., Spintronics; Nature Mater. 2012, 11, 367.
7) Brataas, A.; Kent, A. D.; Ohno, H., Current-induced torques in magnetic materials; Nature Materials 2012, 11, 372.
8) Butenko, A. B.; Leonov, A. A.; Rößler, U. K.; Bogdanov, A. N., Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets; Physical Review B 2010, 82, 052403.
9) Schmitt, A. L.; Higgins, J. M.; Szczech, J. R.; Jin, S., Synthesis and Applications of Metal Silicide Nanowires; J. Mater. Chem. 20 (2010), 223-235
10) Higgins, J. M.; Ding, Ruihua; DeGrave, J. P.; Jin, S., Signature of Helimagnetic Ordering in Single-Crystal MnSi Nanowires; Nano. Lett. 10 (2010), 1605-1610
11) DeGrave, John P.; Schmitt, Andrew L.; Selinsky, Rachel S.; Higgins, Jeremy M.; Keavney, David J.; Jin, Song, Spin Polarization Measurement of Homogeneously Doped Fe1-xCoxSi Nanowires by Andreev Reflection Spectroscopy, Nano Lett., 2011, 11, 4431-4437
12) Yu, X.; DeGrave, J. P.; Hara, Y.; Hara, T.; Jin, S.; Tokura, Y., Observation of the Magnetic Skyrmion Lattice in a MnSi Nanowire by Lorentz TEM; Nano Letters 2013, 13, 3755.
13) John P. DeGrave , Dong Liang , and Song Jin; A General Method to Measure Hall Effect in Nanowires: Examples of FeS2 and MnSi; Nano Lett. 2013, 13 (6), pp 2704–2709.
14) Du, H.; DeGrave, J. P.; Xue, F.; Liang, D.; Ning, W.; Yang, J.; Tian, M.; Zhang, Y.; Jin, S., Highly Stable Skyrmion State in Helimagnetic MnSi Nanowires; Nano Letters 2014, 14, 2026.
15) Du, H.; Liang, D.; Jin, C.; Kong, L.; Stolt, M. J.; Ning, W.; Yang, J.; Xing, Y.; Wang, J.; Che, R.; Zang, J.; Jin, S.; Zhang, Y.; Tian, M., Electrical probing of field-driven cascading quantized transitions of skyrmion cluster states in MnSi nanowires; Nature Communications 2015, 6, 7637.
16) Kanazawa, N.; Kubota, M.; Tsukazaki, A.; Kozuka, Y.; Takahashi, K. S.; Kawasaki, M.; Ichikawa, M.; Kagawa, F.; Tokura, Y., Discretized topological Hall effect emerging from skyrmions in constricted geometry; Physical Review B 2015, 91, 041122.
17) Mehlin, A.; Xue, F.; Liang, D.; Du, H. F.; Stolt, M. J.; Jin, S.; Tian, M. L.; Poggio, M., Stabilized Skyrmion Phase Detected in MnSi Nanowires by Dynamic Cantilever Magnetometry; Nano Letters 2015, 15, 4839.
Publications
1) Xiuzhen Yu, John P. DeGrave, Yuka Hara, Toru Hara, Song Jin, and Yoshinori Tokura; Observation of the Magnetic Skyrmion Lattice in a MnSi Nanowire by Lorentz TEM Nano Lett. 2013, 13 (8), pp 3755–3759.
2) Haifeng Du, John P. DeGrave, Fei Xue, Dong Liang, Wei Ning, Jiyong Yang, Mingliang Tian, Yuheng Zhang, and Song Jin; Highly Stable Skyrmion State in Helimagnetic MnSi Nanowires, Nano Lett., 2014, 14 (4), pp 2026–2032.
3) A. Mehlin, F. Xue, D. Liang, H. F. Du, M. J. Stolt, S. Jin, M. L. Tian, and M. Poggio, Stabilized Skyrmion Phase Detected in MnSi Nanowires by Dynamic Cantilever Magnetometry, Nano Lett., 2015, 15(7), pp 4839-4844, DOI: 10.1021/acs.nanolett.5b02232
4) Haifeng Du, Dong Liang, Chiming Jin, Lingyao Kong, Matthew J. Stolt, Wei Ning, Jiyong Yang, Ying Xing, Jian Wang, Renchao Che, Jiadong Zang, Song Jin, Yuheng Zhang, and Mingliang Tian, Electrical probing of field-driven cascading quantized transitions of skyrmion cluster states in MnSi nanowires, Nat. Comm., 2015, 6, doi:10.1038/ncomms8637
5) Dong Liang, John P. DeGrave, Matthew J. Stolt, Yoshinori Tokura and Song Jin, Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect, Nature Communications, 2015, 6, Article number: 8217, doi:10.1038/ncomms9217
6) Dong Liang, Matthew J. Stolt and Song Jin, Metastable skyrmions: Beat the heat, Nature Physics, 2016, 12, 25–26, DOI: 10.1038/nphys3547
7) Matthew J. Stolt , Zi-An Li, Brandon Phillips, Dongsheng Song, Nitish Mathur, Rafal E. Dunin-Borkowski, and Song Jin, Selective Chemical Vapor Deposition Growth of Cubic FeGe Nanowires That Support Stabilized Magnetic Skyrmions, Nano Lett., 2017, 17, 508–514, DOI: 10.1021/acs.nanolett.6b04548
8) Matthew J. Stolt , Xavier Sigelko, Nitish Mathur, and Song Jin, Chemical Pressure Stabilization of the Cubic B20 Structure in Skyrmion Hosting Fe1–xCoxGe Alloys, Chem. Mater., 2018, 30, 1146–1154. DOI: 10.1021/acs.chemmater.7b05261
9) S. Schneider, D. Wolf, M. J. Stolt, S. Jin, D. Pohl, B. Rellinghaus, M. Schmidt, B. Büchner, S. T. B. Goennenwein, K. Nielsch, and A. Lubk, Induction Mapping of the 3D-Modulated Spin Texture of Skyrmions in Thin Helimagnet, Phys. Rev. Lett. 2018, 120, 217201. DOI: 10.1103/PhysRevLett.120.217201
10) Maxime Leroux, Matthew J. Stolt, Song Jin, Douglas V. Pete, Charles Reichhardt, and Boris Maiorov, Skyrmion Lattice Topological Hall Effect near Room Temperature, Scientific Reports, 2018, 8, 15510 DOI: 10.1038/s41598-018-33560-2
11) Matthew J. Stolt, Sebastian Schneider, Nitish Mathur, Melinda J. Shearer, Bernd Rellinghaus, Kornelius Nielsch, Song Jin, Electrical Detection and Magnetic Imaging of Stabilized Magnetic Skyrmions in Fe1−xCoxGe (x < 0.1) Microplates, Adv. Funct. Mater., 2019, 29, 1805418 DOI: 10.1002/adfm.201805418
12) Nitish Mathur, Matthew J. Stolt, Kodai Nitsu, Xiuzhen Yu, Daisuke Shindo, Yoshinori Tokura, and Song Jin. Electron Holography and Magnetotransport Measurements Reveal Stabilized Magnetic Skyrmions in Fe1-xCoxSi Nanowires. ACS Nano, 2019. DOI: 10.1021/acsnano.9b02130
Our previous research on

